Author: Goran Sukovic, PhD in Mathematics, Faculty of Natural Sciences and Mathematics, University of Montenegro![]()
One of the most common questions from my students when they start to learn computer science is, “We are studying for a Computer Science major. Why we have to learn mathematics?” Recently, the question is slightly different. “I want to be a data scientist/machine learning expert. Why do we have to learn the mathematics behind machine learning algorithms? We can build models using the libraries available in Python or R or any other language.” This kind of issue creates false expectations among aspiring students. In my experience, there are many reasons for this. Mathematics can be quite intimidating and challenging, especially for students coming from a non-technical background. Students also show some kind of “programming laziness,” thanks to the vast body of open source machine learning and deep learning frameworks. A lot of students easily create different models, but have trouble in comparing models or interpreting the results and/or parameters of the chosen model.
If you want to become a good machine learning engineer or data scientist, you need to understand the mathematics behind machine learning. To design, develop, and debug machine learning systems, we have to understand how the algorithms really work. But I think that mathematics is not the primary prerequisite for machine learning, especially if your primary goal is to work in industry or business. You can create a business value using “off the shelf” algorithms and libraries. Available libraries will keep mathematics out of your sight. To get started mastering practical machine learning, an entry level machine learning engineer/data scientist needs to have at least as much math skill as a college freshman. In an academic or research environment, you have to develop a deep understanding of the math behind machine learning algorithms.
According to an excellent book Mathematics for Machine Learning (freely available for download) a set of fundamental machine learning algorithms is (Figure 1):
1. Regression
2. Density estimation
3. Dimensionality reduction
4. Classification
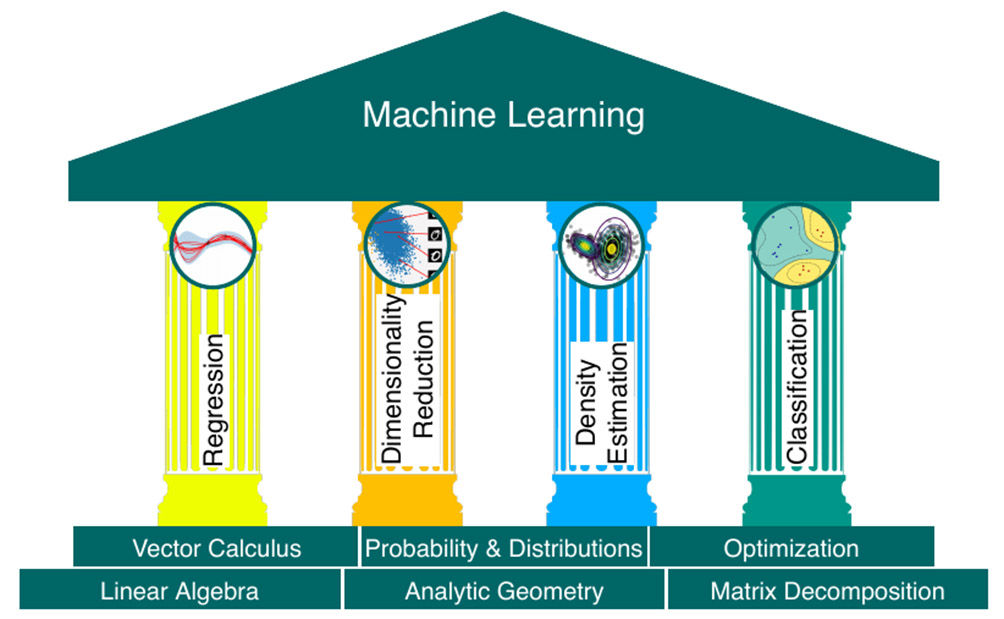
From a high level, there are the following mathematical areas in machine learning:
1. Linear Algebra
2. Probability and Statistics
3. Multivariate Calculus
4. Optimization Theory
Numerical data can be represented as vectors, and a table of such data can be represented as a matrix. The study of vectors and matrices is called linear algebra. Vector similarity and distances are subjects of analytical geometry. Matrix decomposition and transformations allow an intuitive interpretation of the data and more efficient learning. We often would also like to quantify the confidence we have about the value of the prediction, which can be expressed using probability theory. Training machine learning models typically require finding parameters that maximize some performance measure. Multivariate calculus (or vector calculus) and optimization are necessary mathematical tools.
Linear Algebra comes up everywhere in machine learning and data science. Skyler Speakman recently said that “Linear Algebra is the mathematics of the 21st century.” To understand how machine learning algorithms work, you can use following topics from Linear Algebra (the list is not exclusive):
∘ Vector Spaces and Norms
∘ Projections and Subspaces
∘ Linear Operators, Eigenvalues, and Eigenvectors
∘ Matrix Operations
∘ Orthogonalization and Orthonormalization
∘ Symmetric Matrices
∘ Eigendecomposition of a Matrix
∘ Principal Component Analysis (PCA)
∘ Singular Value Decomposition (SVD), LU Decomposition, QR Decomposition/Factorization
There are so many online resources about Linear Algebra to delve into. You can check online courses offered by MIT Courseware (Prof. Gilbert Strang), Khan Academy’s Linear Algebra, The Essence of Linear Algebra, or an excellent book, Linear Algebra Done Right. You can find examples of applications of Linear Algebra in Computer Science on codingthematrix.com.
Many machine learning algorithms are based on probability. Furthermore, to verify models, we often use statistical methods. Probability and statistic topics include:
∘ Combinatorics
∘ Probability Rules and Axioms
∘ Bayes’ Theorem
∘ Random Variables, Variance, and Expectation
∘ Conditional and Joint Distributions
∘ Maximum Likelihood Estimation (MLE), Prior and Posterior, Maximum a Posteriori Estimation (MAP)
∘ Sampling Methods
∘ Hypothesis Testing, Confidence Interval
For a deeper understanding of probability and statistics check Khan Academy’s Probability and Statistics, Harvard Stat 110 course (with the free online version of the book Introduction to Probability by Joe Blitzstein and Jessica Hwang), or the book All of Statistics: A Concise Course in Statistical Inference. For a short and abstract introduction, check this article “The mathematical foundations of probability”.
If you are in the deep learning or use gradient descent, then you are already using Multivariate Calculus. Many machine learning algorithms are based on the following topics:
∘ Vector-Valued Functions
∘ Differential and Integral Calculus
∘ Partial Derivatives and Gradient
∘ Hessian, Jacobian, Laplacian, and Lagrangian.
For a detailed introduction to multivariate calculus check MIT online course Multivariate Calculus.
For most of the machine learning algorithms, training the model is done by finding parameters that maximize some performance measures. Optimization is one of the main components of machine learning. Most machine learning algorithms build an optimization model and learn the parameters in the objective function from the given data. Topics are:
∘ Gradient Descent
∘ Constrained Optimization and Lagrange Multipliers
∘ Convex Optimization.
For further information check Boyd and Vandenberghe’s course on Convex Optimization from Stanford or Khan Academy’s Optimization. For the math behind the deep learning, check Dive into Deep Learning, Deep Learning Book, or Grokking Deep Learning.
Other math topics not covered in the four major areas described above include:
∘ Sets and Sequences
∘ Topology
∘ Limits
∘ Fourier Transforms
∘ Information Theory (Entropy, Information Gain)
∘ Function Spaces and Manifolds
∘ Algorithm Complexity and Data Structures
Recently, there has been an explosion in the area of open source machine learning libraries such as scikit-learn, Weka, Tensorflow, R-caret, etc. There are many reasons why mathematics is important for machine learning engineers/researchers. Math can help you with the following issues:
1. How to select an appropriate model, taking into account the number of parameters, number of features, accuracy, training time, and model complexity?
2. How to set the model’s parameters?
3. How to choose validation strategies?
4. How to understand the Bias-Variance tradeoff to identify underfitting and overfitting?
5. How to estimate confidence interval and uncertainty?
The main question is the amount of math necessary and the level of math needed to understand machine learning.
For a more academic approach to Mathematics for Machine Learning check the math review notes from Berkeley’s CS189/289A or Stanford CS229. Also, there are a couple of excellent books such as
An Introduction to Statistical Learning: with Applications in R (Springer Texts in Statistics Book 103) or Applied Predictive Modeling. For a more mathematical approach to the subject please take into consideration The Elements of Statistical Learning: Data Mining, Inference, and Prediction or a brand new bčook from Cambridge University Press, Mathematics for Machine Learning (available online).
For the people always in rush, we also compiled some of our favorite Math Formula Sheets!
Linear Algebra

Source: https://minireference.com/static/tutorials/linear_algebra_in_4_pages.pdf
Calculus

Source: http://tutorial.math.lamar.edu/getfile.aspx?file=B,41,N
Probability
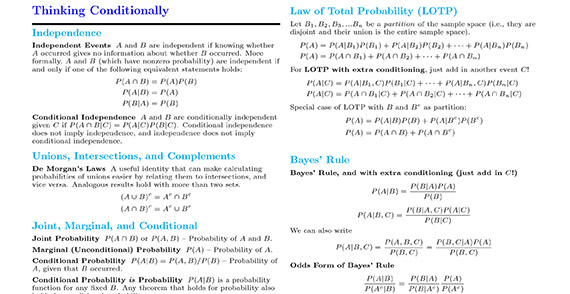
Source: http://www.wzchen.com/s/probability_cheatsheet.pdf
Data Science
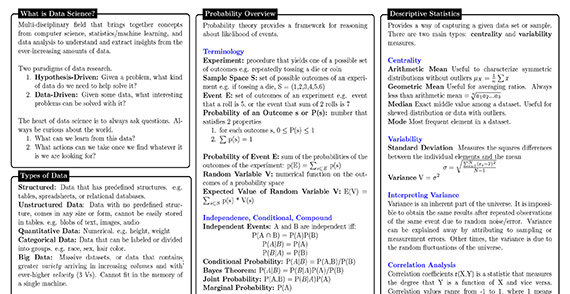
Source: https://www.datasciencecentral.com/profiles/blogs/new-data-science-cheat-sheet
Thanks for reading this article. If you like it, please recommend and share it.
